モーター負荷トルクＴは下記式で求められます。

​

  Ｔ=Ｔr(加速トルク)+Ｔc(外的負荷トルク）

　　　　　　　　　　※外的負荷トルクは主に摩擦トルクのことです。

​

　　【回転系負荷トルク】                                                 ​　　【直動系負荷トルク】

​

​　　　Ｔ= 〔Ｉr x (ﾓｰﾀｷﾞﾔ/ﾜｰｸｷﾞﾔ)^2〕 x ω'                             Ｔ= Ｉc  x ω'

                （ﾓｰﾀｷﾞﾔ/ﾜｰｸｷﾞﾔ）の2乗                                   但し、Ic=Jc/ｇで、Jc=Mc x (A/2π)＾2　です。

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（Ａ/2π）の2乗

 

　それぞれを求めてみましょう。

​

​

●まずは、加速度によって生じる物体のイナーシャによる負荷トルク(Ｔr)を求めます。

　この時、回転系の負荷と直動系の負荷に分けて考えます。

​

　回転運動系のイナーシャは、＜モーターギヤ、従動ギヤ、アーム＞になります。

　直動運動系のイナーシャは、＜ワーク＞になります。

​

　　・回転運動系ｲﾅｰｼｬIr　(g･cm･s2)

　　　　Ir=(GD^2/4)/g=Jr/g

 

　　　　ここで、Jr=　Mr x K＾2　=　Mr x (r^2/2)　(g･cm2)

                    　　　　（Kの2乗）　　　　（rの2乗/2）

 

　　　　但し、Mr：質量(ｷﾞﾔの質量)　(g)　　r：回転半径(ｷﾞﾔの半径)　(cm)

                   g：重力加速度　980　(cm/s2)

        より、

​

　　　　Ir（従動ｷﾞﾔ）=10x(2x2/2)/980=0.02　(g･cm･s2)　　　　　  Ir（従動ｷﾞﾔ）=0.02　(g･cm･s2)

​

　　　　Ir（ﾓｰﾀｰｷﾞﾔ）=15x(3x3/2)/980=0.07　(g･cm･s2)　 　　　 Ir（ﾓｰﾀｰｷﾞﾔ）=0.07　(g･cm･s2)

　　　　

　　　　次に、Ir（ｱｰﾑ）を求めます。

　　　　同じ回転運動系のｲﾅｰｼｬですが、長方形の場合、K^2は下記になります。

​

　　　　K^2=(a^2+b^2+12xL^2)/12

　　　　（↑Kの2乗=（aの2乗+bの2乗+12xLの2乗）/12）

​

　　　　

 

　　　　但し、aは長方形の幅（cm）、bは長さ（cm）

　　　　また、回転軸が重心X0から外れるX1軸の場合、LはX0軸とX1軸の距離(cm）

　　　　

　　　　形状により、K^2は異なりますので、計算の際には注意が必要です。

　

​

​

​

         ここでは、L=5(cm)とします。

　　　　実際の設計業務においては、重心はCADで簡単に求めたられますのでそれを活用したりします。

　　　　

        Ir（ｱｰﾑ）=(80 x (2x2 + 14x14 + 12x5x5)/12)/980 =3.4 

                                                                               　　　　　 Ir（ｱｰﾑ）=3.4　(g･cm･s2)

   

 

　 

　　・直動運動系ｲﾅｰｼｬIc　(g･cm･s2)　を求めます。

　　　　Ic=(GD2/4)/g=Jc/g

 

　　　　ここで、

 　　直動運動する物体のイナーシャ（慣性モーメン）の式

　　　　　　　　　　　　　　↓

　　　　　Jc=Mc x (A/2π)＾2　(g･cm2)

　　　　　　　　　（A/2π）の2乗

　　　　　　　　       

　　　　但し、Mc：質量(ﾜｰｸの質量)　(g)　　g：重力加速度　980　(cm/s2)

                 A：単位移動量　(cm/rev)　

　　　　　　　　　　　　　　　　　　　↑単位:ﾓｰﾀｰ1回転当たりの移動量(cm)

　　　　より、

​

　　　　Ic=(330)ｘ(16.5/2ｘπ)ｘ(16.5/2ｘπ)/980=2.32　(g･cm･s2)　　　　　Ic=2.32　(g･cm･s2)　

​

 

　　　　よって、加速トルクTrは、

　

　　　　回転系（従動ギヤ）の加速トルク：　Ｔr= Ir x(ﾓｰﾀｷﾞﾔ/ﾜｰｸｷﾞﾔ)^2 x ω'=0.02 x (3/2)x(3/2) x ω'

　 　　　　　　　　　　　　　        　　　　　　　　　　＜補足：↑従動ギヤが対象で、モーターギヤは直結してるので、ギヤ比は１＞

　　　　

　　　　回転系（モーターギヤ）の加速トルク：　Ｔr= Ir x ω'=0.07 x ω'

　　　　

　　　　回転系（アーム）の加速トルク：　Ｔr= Ir x(ﾓｰﾀｷﾞﾔ/ﾜｰｸｷﾞﾔ)^2 x ω'=3.4 x (3/2)x(3/2) x ω'

​

​

​

 

　　　　ギヤ比（3/2=1.5倍）により、アームの揺動量は、1.5倍になっています。

　　　　イナーシャはギヤ比の2乗に比例するので、アームのイナーシャは、1.5ｘ1.5=2.25倍になります。

　　　　　　　　　　

 

 

 

　　　　直動系の加速トルク：　Ｔr= Ic xω'=2.32xω'

     

​

　　　　但し、Ir　：回転運動系　ｲﾅｰｼｬ　(g･cm･s2)　　Ic　：直動運動系　ｲﾅｰｼｬ　(g･cm･s2)　

　　　　　　　ω' ：モーター　角加速度　(rad/s2)

​

​

●ω'を求めます。

 

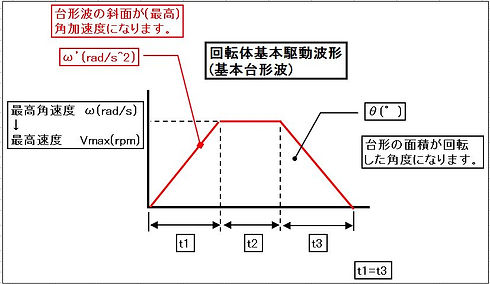
　　　(最高)角加速度ω'　(rad/s2)

　　　基本駆動波形は、右図のような基本台形波です。

​

​

　　　まずは最高角速度ωを求めます。

 

　　　回転角度は台形の面積となるので、

       ωx(t1+t2)=θxπ/180　(rad/s)

　　　但し、

       t1、t2はX軸の時間　(s)　θは回転角度　(°)

​

　　　ω=θxπ/（180x（t1+t2））　(rad/s)

　　　より、

　　　ω=360xπ/(180x(0.05+0.35))=15.7　(rad/s)　

 

　　　ここで、求める最高角加速度ω'は台形波の斜辺となります。

　　　よって、

 

　　　ω'=ω/t1=〔θxπ/180x（t1+t2）〕/t1　　(rad/s2)

　　　より、

　　　ω'=15.7/0.05=314　(rad/s2)　　　　　　　　　　　　　　　　　　　　　　ω'=314　(rad/s2)

​

　　

　　　よって、

　　　回転系の加速トルク（従動ギヤ）：Ｔr=Ir ｘ（ﾓｰﾀｷﾞﾔ/ﾜｰｸｷﾞﾔ）^2 x ω' 　

　　　　　　　　　　　　　　　　　                 　　　=（0.02) x (3/2) ｘ　(3/2) x 314 =14.13 (g・cm)

 　

      回転系の加速トルク（モーターギヤ）：Ｔr=Ir x ω' =0.07 x 314 =21.98 (g・cm)

​

　　  回転系の加速トルク（アーム）：Ｔr=Ir ｘ（ﾓｰﾀｷﾞﾔ/ﾜｰｸｷﾞﾔ）^2 x ω' 　

　　　　　　　　　　　　　　　　　                 　　　=（3.4) x (3/2) ｘ　(3/2) x 314 =2402.1  (g・cm)

                                  　　

​

　 　 直動系の加速トルク：Ｔr=Ic xω' =2.32x314=728.48 (g･cm)

　　　

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　回転系の加速トルク　Tr=2438.21　(g･cm)

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　直動系の加速トルク　Tr=728.48　(g･cm)

​

​

​

      このように、加速に伴うトルクが、とても大きな数値になっています。

　　　これは、加速時間が0.05sという短い時間で加速させていることと、運動量をギヤ比により増加させたことによって、

　　　イナーシャがギヤ比の2乗で効いてきたため、このような数値になっていることが、分かると思います。

　　　また、このような場合、使用するモーターによって、負荷イナーシャとモーター許容イナーシャを比較し、チェックを

　　　行うことが大切な場合もありますので、注意が必要です。

​

​

​

​

​

●次に外的負荷(バネや摩擦など)によって生じる物体の外的負荷トルク(=摩擦トルク)Ｔcを求めます。

　　補足：ぜんまいバネの力Fsは250（gf）で、常に一定の力でワークを上側に引っ張り上げていることとします。

　

　　直動運動する外的負荷トルク（摩擦トルク）の式

　　　　　　　　　　　　　　↓

      Ｔc=F x D/(2 x n x i)　　（g･cm）

 　　　　　　

　　水平の場合：F=Fa　　　　+　　μx N

　　　　　　　　　　　　↑バネ力など　　↑摺動抵抗（Ｎは垂直抗力）

   

　　傾きがある場合：F=Fa　     +　    mg x (sinθ     +       μcosθ)　　　　　　　　　←（μx Nを分解した式）

　　　　　　　　　　　　　　 ↑バネ力など　          ↑傾き方向の力　    ↑垂直方向の力

 

     但し、F：直動運動方向の力　(gf)　　 D：モーターギヤ直径　(cm)    n：効率(0.85～0.95)　　 i：減速比

　　　　　　　　Fa：外力(バネなど)　　(gf)　　μ：摺動面の摩擦係数(0.05)　　N：垂直方向荷重(=mg)　(gf)

　　　　　　m：ワークとラックの総質量　(g)　　g：重力加速度　980　(cm/s2)　　θ：傾き角度　(°)

​

​

　　

　　では、まずはＦを求めます。

​

　　垂直なので、F=Fa+μN　のN（＝垂直抗力）は、”0”になります。

​

　　ここで、Faを考えます。

　　Faは、バネ力などの負荷になりますが、この場合、バネ力が一定のため、ワークとバネ力の差が、総質量となり、負荷

　　になります。

　　今回の例題の場合、バネ力が常に一定で、且つ、ワークを上側に引っ張り上げていることを念頭に、上り、下りのそれ

　　ぞれの加速、減速時において、負荷を助ける側になるのか、負荷を掛ける側になるのか、を考慮する必要があります。

　　本例題のようにバネ力が常に一定で且つワークを引っ張り上げている場合は、

​

　　Fa= Fs 　　　　+　　W　＝　-250　+　330　＝　80（gf）　になります。

 　　　　↑バネ力　　　↑負荷となる総質量

​

    ここで、〔上り〕と〔下り〕でFaは異なることに注意します。

​

　　●〔上り〕の加速時は、"＋"になります。⇒　(トルクを助けない方向<モーターに負荷をかける方向>)

　　●〔上り〕の減速時は、"－"になります。⇒　((トルクを助ける方向<モーターに負荷をかける方向>)　　　

　　●〔下り〕の加速時は、"－"になります。⇒　(トルクを助ける方向<モーターに負荷をかけない方向>)　

​　　●〔下り〕の減速時は、"＋"になります。⇒　（トルクを助けない方向<モーターに負荷をかける方向>）

　　

　　より、〔上り〕と〔下り〕に分けてそれぞれのＦaを求めます。

　

　　モーターに負荷をかける方向：〔上りの加速時〕〔下りの減速時〕　Fa＝＋80（gf）

　　モーターの負荷を助ける方向：〔上りの減速時〕〔下りの加速時〕　Fa＝－80（gf）

　　

　　⇒モーターに最大負荷をかけるのは、〔上りの加速時〕

​

　　よって、

　　直動運動する外的負荷トルク（摩擦トルク）は、Ｔc=F x D/(2 x n x i)　　（g･cm）より、

​

　　　Ｔc　=　80  　 x  （3ｘ2）/（2 x 0.95 x  3/2)  = 480/2.85 = 168.42

               ↑F(上り)　↑D　　　　 ↑n　　↑ｷﾞﾔ比(=ﾓｰﾀｷﾞﾔ/従動ｷﾞﾔ)

                                                                                                      Tc=168.42（g・cm）

ここで、上述で計算した結果をまとめます。

​

　　回転系の加速トルク　Tr=2438.21　(g･cm)

　　直動系の加速トルク　Tr=728.48　 (g･cm)

　　外的(摩擦)負荷トルク(上り）　Tc=168.42 (g･cm)

​

​

”上り”の加速時に発生する、モーター最大負荷トルクは、

​

　　　　Ｔ=　Tr　　　　　　　+　　　　　　　　Tc

　　　　　　↑回転&直動系の加速トルク　　↑外的負荷トルク(=摩擦トルク)

　　　　より、

　　　　T=(2438.21+728.48)+168.42=3335.11 (g･cm)　　　　　　モーター最大負荷トルクT=3335.11(g･cm)

​

​

​

​

​

 

このように、モーター最大負荷トルクの多くを加速トルクが占める場合、実際の駆動制御においては、下降時と上昇時の

速度を変更（下降時は速く、上昇時は遅く、など）したり、加減速時間を見直したり、バネ力やワーク質量を見直しするなど

して、負荷トルクを調整したりするのが一般的な手法だと思いますが、場合によっては、計算された負荷を満たすモーター

を選定しなければならない場合もあり、実業務では、それぞれの条件下により、異なってくると思います。

​

いずれにせよ、このように計算をしておくこで、どこを調整すれば、効率よく負荷トルクを調整できるのか、を視覚化できる

ことは、計算するメリットの１つであると言えるでしょう。

​